Authors: Logan Burnett and Cheng-Chien Chen
Department of Physics
INTRODUCTION: Density functional theory (DFT) is a widely used method for calculating the electronic properties of materials. The method is based on the idea of approximating the many-electron wave function using the ground state electron density. While DFT is a very powerful tool, it has limitations, particularly when dealing with strongly correlated systems.1 One way to address this issue and improve predictions is to introduce a correction term, known as the Hubbard U parameter, which accounts for the on-site Coulomb interactions among electrons in localized d or f orbitals.1 In this report, we will discuss the importance of the Hubbard U parameter in DFT calculations, and research involving the calculation of the Hubbard U parameter of rare-earth materials using first-principles software and linear response theory.
The Hubbard Model
The Hubbard model is a simplified model of interacting electrons in a lattice system, first proposed by John Hubbard in 1963.2 The model assumes that each site in the lattice has a single orbital, and the electrons can hop between adjacent sites with a hopping parameter t. The model also includes an on-site Coulomb repulsion term U, which accounts for the interaction between two electrons occupying the same site.
The Hamiltonian for the Hubbard model is given by:
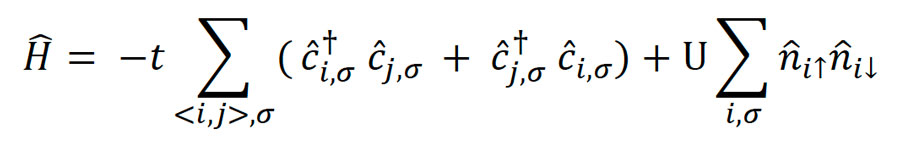
Here, 𝑐̂†𝑖,𝜎 and 𝑐̂𝑖,𝜎 are the creation and annihilation operators for an electron with spin σ at site i, 𝑛̂𝑖↑ and 𝑛̂𝑖↓ are the number operators for up and down spins, respectively, and the sum ⟨i,j⟩ runs over adjacent sites.2
The Hubbard model is a many-body problem that cannot be solved exactly for complex systems. However, there are several approximations that can be used to study the properties of the system. One common approach is the mean-field approximation, in which the electron-electron interactions are approximated by a static mean field. This mean field can be self-consistently determined by solving the resulting single-particle Schrödinger equation. Another approach is the dynamical mean-field theory (DMFT), which treats the local correlations exactly and approximates the non-local correlations with a mean field. In DMFT, the lattice problem is mapped onto a single-impurity problem, which can be solved exactly using numerical techniques.3
The Hubbard model has been used extensively to study strongly correlated electron systems, particularly those involving localized d or f electrons. In these systems, the on-site Coulomb repulsion U can be very large, leading to the breakdown of traditional band theory.
In density functional theory calculations, the Hubbard U parameter is introduced as a correction term to account for the on-site Coulomb interactions among electrons in localized d or f orbitals, which are typically strongly correlated. The value of the Hubbard U parameter depends on the specific material being studied and can be obtained by fitting the calculated band structure to experimental data or by using first-principles methods, such as linear response theory.
The Hubbard U Parameter in Density Functional Theory Calculations
The Hubbard U parameter is an empirical correction term that is added to the DFT Hamiltonian. It accounts for the on-site Coulomb interaction among electrons in localized d or f orbitals, which are typically strongly correlated. The inclusion of the Hubbard U parameter is necessary for obtaining accurate electronic and magnetic properties of materials that involve localized d or f electrons.
The Hubbard U parameter is usually calculated by comparing the calculated band structures of a material with experimental data. However, in the absence of experimental data, the Hubbard U parameter can be calculated using first-principles methods. One such method is the linear response theory, which involves calculating the response of the electronic structure of a material to an external perturbation. The Hubbard U parameter can then be obtained by fitting the response function to a model.
Importance of Rare-Earth Metals
Rare-earth metals are a group of elements located near the bottom of the periodic table that have unique electronic and magnetic properties. These metals have a broad range of applications in modern technology, including in the production of high-strength magnets, optical fibers, electronic devices, and catalytic converters.4
Rare-earth metals are also widely used in the production of optical fibers. The fibers are essential components of modern telecommunications networks and help provide high-speed data transmission over long distances. Erbium is particularly important for this application, as it is used to amplify optical signals in fiber optic amplifiers.4
Another important application of rare-earth metals is in electronic devices, such as solid-state computer hard drives and cell phones. Gadolinium, another rare-earth metal, is used in the production of magneto-optical storage devices,4 which can store much larger amounts of data than traditional hard drives.
Rare-earth metals are also used as catalysts in a variety of chemical reactions, including the production of petroleum and the removal of harmful pollutants from exhaust gases. Cerium is an integral component of this application, as it is used to convert harmful pollutants, such as carbon monoxide and nitrogen oxides, into less harmful substances.4
Calculation of the Hubbard U Parameter for Rare-Earth Metals
Our research involves the calculation of the Hubbard U parameter of cerium, terbium, and erbium using first-principles software and linear response theory.5 The first-principles software used is the Vienna Ab-Initio Simulation Package (VASP), which employs DFT to calculate the ground state properties of materials. The calculations are performed on the Frontera supercomputer located at the University of Texas at Austin and the Perlmutter supercomputer located at the University of California, Berkeley. To ensure proper convergence of the Hubbard U parameter, the calculations are performed on unit cell sizes ranging from 2 to 72 atoms. Additionally, calculations are also performed to determine how the Hubbard U evolves as a function of pressure, volume, and lattice parameter compression. These calculations are particularly important as rare-earth materials are being found to have novel applications in high-pressure environments.
Thus far, we have obtained a value of the Hubbard U for cerium supercells up to 36 atoms. The required convergence criteria and k-points density was much higher than predicted, making the calculations more computationally expensive and time consuming. Nonetheless, linear response theory was successfully applied to cerium and the data was fit to a linear plot.
Figure 1: Linear Response Functions for Ce Supercell
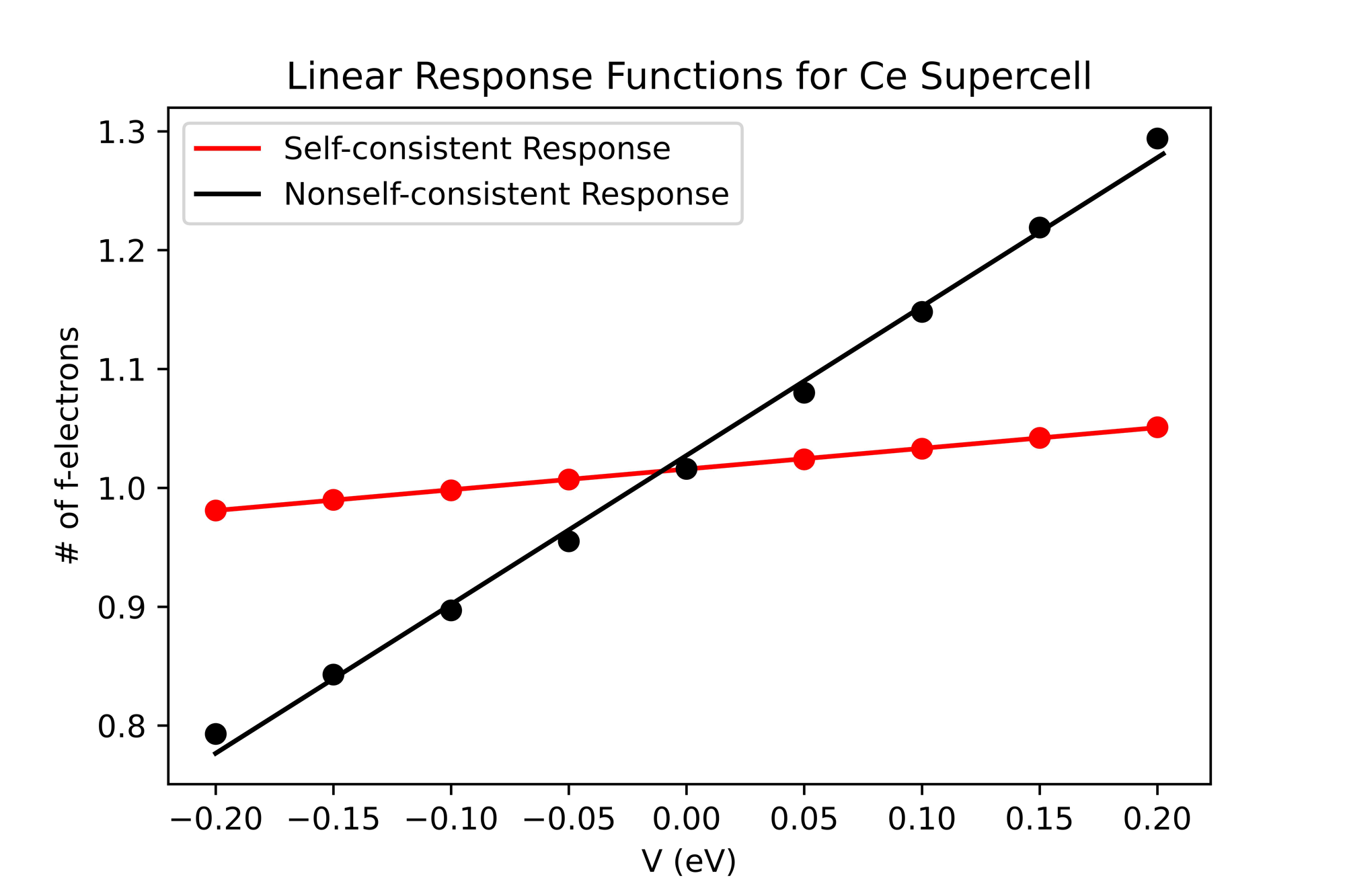
Figure 1. The Self-consistent (red) and Nonself-consistent (black) linear response functions for an 18-atom cerium supercell. The number of f-electrons is easily approximated as linearly proportional to the applied perturbation potentials.
Following, the process will be extrapolated to a maximum unit cell size of 72 cerium atoms. The computational time appears to scale exponentially with increasing atoms per unit cell, with many of the calculations already requiring thousands of CPUs and multiple hours on the Frontera and Perlmutter supercomputers. Once fully converged, the next step will be to investigate the behavior of the cerium Hubbard U as a function of pressure, cell volume, and lattice parameter compression.
Figure 1 - Accessible Data Table
-
Click to Expand
Figure 1: Linear Response Functions for Ce Supercell
V (ev)
Number of Electrons:
Self-consistent linear responseNumber of Electrons:
Nonself-consistent linear response-.20
0.981
0.793
-.15
0.990
0.843
-.10
0.998
0.897
-.05
1.007
0.955
0.00
1.016
1.016
0.05
1.024
1.080
0.10
1.033
1.148
0.15
1.042
1.219
0.20
1.051
1.294
Conclusions
The Hubbard U parameter is an essential correction term in DFT calculations, particularly when dealing with strongly correlated systems involving localized d or f electrons. Including the Hubbard U parameter into DFT is necessary for accurately predicting the electronic and magnetic properties of strongly correlated materials. This project involving the calculation of the Hubbard U parameter of cerium, terbium, and erbium using first-principles software and linear response theory is an important step towards improving understanding of the electronic and magnetic properties of rare-earth materials, particularly in high-pressure environments.
References
- Tolba, S.A., Gameel, K.M., Ali, B.A., Almossalami, H.A., and Allam, N.K. (2018). "The DFT+U: Approaches, Accuracy, and Applications." Density Functional Calculations - Recent Progresses of Theory and Application, edited by Gang Yang, InTechOpen, doi:10.5772/intechopen.72020.
- Hubbard, J. “Electron Correlations in Narrow Energy Bands.” Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, vol. 276, no. 1365, 26 Nov. 1963, pp. 238–257.
- Backes, S., Murakami, Y., Sakai, S., and Arita, R. (2023). Dynamical mean-field theory for the Hubbard-Holstein model on a quantum device. Phys. Rev. B, 107, 165155, doi :10.1103/PhysRevB.107.165155.
- Balaram, V. "Rare Earth Elements: A Review of Applications, Occurrence, Exploration, Analysis, Recycling, and Environmental Impact." Geoscience Frontiers, vol. 10, no. 4, 2019, pp. 1285–1303.
- Cococcioni, M., and de Gironcoli, S. "Linear Response Approach to the Calculation of the Effective Interaction Parameters in the LDA+U Method." Phys. Rev. B, vol. 71, American Physical Society, Jan. 2005, p. 035105.
